Pembahasan: Peluang Adalah ~ Garenggati
Dimana ada kemauan disitu ada jalan. Pepatah ini memang terlihat sepele, tapi bermakna sangat dalam. Buktinya Anda berhasil menemukan informasi mengenai Peluang Adalah yang sengaja kami hadirkan untuk sobat pembaca semuanya. Disini kita akan mengulasnyya secara lengkap dan menuliskannya dengan bahasa yang mudah dimengerti sehingga akan lebih mudah dalam memahaminya. Oke langsung disimak aja yuk.
Uraian Lengkap Peluang Adalah
Selamat datang di Dosen.co.id, web digital berbagi ilmu pengetahuan. Kali ini PakDosen akan membahas tentan Peluang? Mungkin anda pernah mendengar kata Peluang? Disini PakDosen membahas secara rinci tentang pengertian, sejarah, rumus, batas, teori, nilai dan contoh. Simak Penjelasan berikut secara seksama, jangan sampai ketinggalan.

Pengertian Peluang
Peluang atau dikenal juga sebagai probabilitas merupakan cara untuk mengutarakan pengetahuan atau keyakinan bahwa suatu peristiwa akan berlaku atau sudah terjadi. Konsep peluang matematika sudah dirumuskan dengan lebih cermat dalam matematika dan kemudian dipakai secara lebih luas tidak hanya dalam matematika atau statistika, namun juga keuangan, sains dan filsafat. Konsep peluang matematika ini bisa kita temui dalam kehidupan sehari-hari. Semua pasti pernah melihat mata uang logam ataupun koin kan? Mata uang logam tersebut terdiri dari 2 buah sisi. Kita misalkan sisi pertama merupakan angka, sementara sisi kedua merupakan gambar. Apabila uang logam tersebut kita lemparkan ke atas sebanyak satu kali. Berapa peluang munculnya angka? Sementara apabila kita lempar sebanyak 2 hingga 3 kali bahkan 10 kali berapa peluang munculnya angka? Konsep yang demikian dinamakan peluang. Untuk memahami lebih lanjut mari kita pelajari bersama-sama materi peluang matematika, rumus peluang dan beberapa contoh soal beserta penyelesaiannya.
Peluang bisa diartikan sebagai sebuah cara yang dijalankan untuk memahami kemungkinan terjadinya sebuah peristiwa. Dalam setiap permasalahan ada ketidakpastian yang diakibatkan suatu perbuatan yang sekali-kali berdampak lain. Contoh diatasa sebelumnya adalah sebuah mata uang logam yang dilemparkan ke atas dampaknya bisa muncul sisi gambar (G) atau sisi angka (A), maka sisi yang akan muncul tidak bisa dikatakan secara pasti. Dapak melemparkan sebuah mata uang logam tersebut terdapat salah satu dari dua peristiwa yang bisa terjadi yakni munculnya sisi G atau A. Aktivitas melemparkan mata uang logam tersebut dinamakan suatu perbuaatan acak. Tindakan tersebut bisa diulang beberapa kali dan disusun perbuaatan tersebut dinamakan percobaan. Perbuaatan satu kali juga bisa disebut dengan suatu percobaan.
Sejarah Teori Peluang
Teori Peluang (probabilitas) merupakan cabang matematika yang banyak penerapannya dalam kehidupan sehari-hari. Teori Peluang lahir dan berkembang dari dunia hitam (meja perjudian). Pada awal abad ke 17 seorang penjudi bangsawan Perancis bernama CHEVALIER de MERE minta pertolongan kepada BLAISE PASCAL, pertolongan yang diharapkan oleh Chevalier de Mere tidak lain adalah bagaimana caranya agar ia memperoleh kemenangan dalam meja perjudian. Cara-cara untuk memperoleh kemenangan dalam meja perjudian itu merupakan dasar – dasar Teori Peluang yang disarankan oleh Blaise Pascal (1623 – 1662). Dasar – dasar teorema peluang ini selanjutnya dikembangkan oleh PIERRE de FERMAT (1601 – 1665). Teori peluang yang pada saat lahirnya dianggap sebagai ilmu haram, namun dalam perkembangannya banyak mendapatkan restu dari para ahli matematika. Bahkan saat ini, teori peluang mampu memberikan nilai tambah dan memegang peran penting dalam perkembangan Ilmu Pengetahuan dan Teknologi, Ilmu-ilmu social Modern, misalnya :
- Lahirnya teori atom, teori Mekanika Kuantum, teori Radioaktif dalam Fisika Modern.
- Lahirnya teori Fermi – Dirac, teori Boson dalam Fisika Statistik.
- Lahirnya teori Statistika yang banyak penerapannya dalam bidang antropologi dan kependudukan, pertanian, geofisika dan meteorology, transportasi, ekonomi, industri dan lain sebagainya.
Rumus Peluang Matematika
Percobaan melemparkan mata uang logam hasilnya merupakan G atau A. Apabila percobaan dilempar 10 kali dan muncul G 4 kali maka frekuensi relatif munculnya G merupakan 4/10. Apabila percobaan dijalankan 10 kali lagi dan muncul G 3 kali sehingga dalam 20 kali percobaam G muncul sebanyak 7 kali maka frekuensi relatif muncul G pada 20 percobaan merupakan 7/20.
1. Frekuensi Relatif
Frekuensi aadalah perbandingan antara banyaknya percobaan yang dijalankan dengan banyaknya perisitiwa yang diamati. Berikut rumus dari frekuensi relatif, sebagai berikut:

Contoh:
Pada percobaan melempar mata uang logam sebanyak 100 kali ternyata muncul permukaan gambar sebanyak 30 kali. Berapakah frekuensi relatifnya?
Frekuensi relatif muncul gambar = 30/100 = 3/10
2. Peluang

Contoh:
Pada percobaan melempar undi sebuah mata uang logam maka. Peluang muncul angka = 1/2.
3. Ruang Sampel
Ruang sampel adalah gabungan dari semua peristiwa (hasil) percobaan yang mungkin terjadi. Ruang sampel dilambangkan dengan S.
Contoh:
- Ruang sampel pada pelemparan sebuah dadu merupakan S = (1, 2, 3, 4, 5, 6).
- Ruang sampel pada pelemparan sebuah mata uang logam merupakan S = (A, G).
4. Menentukan Ruang Sampel
Ruang sampel hasil dari melempar dua mata uang yang bisa ditetapkan dengan memakai tabel (daftar) seperti berikut:
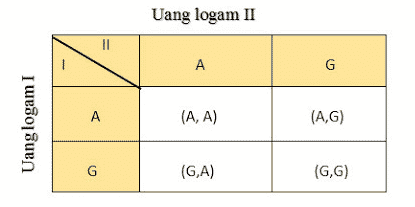
Ruang sampelnya merupakan S = {(A,A), (A,G), (G,A), (G,G)}
Kejadian A1 yang berisi 2 gambar = (G,G)
Kejadian A2 yang tidak berisi gambar = (A,A)
5. Titik Sampel
Titik sampel merupakan anggota-anggota dari ruang sampel
Contoh:
Ruang sampel S = ((A,A), (A,G), (G,A), (G,G))
Titik sampelnya merupakan ((A,A), (A,G), (G,A), (G,G))
6. Peluang Kejadian A atau P(A)
Peluang kejadian bisa ditetapkan dengan cara sebagai berikut:
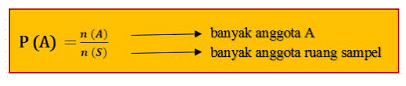
S = {1,2,3,4,5,6} maka nilai n(S) = 6
A = {2,3,5} maka n(A) = 3
Penjelasan tersebut menguraaikan bahwa apabila setiap titik sampel dari anggota ruang sampel S mempunyai peluang yang sama, maka peluang kejadian A yang jumlah anggotanya dinyatakan dalam n(A) bisa dinyatakan dengan rumus sebagai:
7. Nilai Peluang
Nilai-nilai peluang yang didapatkan berpusat antara 0 hingga 1. Untuk setiap kejadian A, batas-batas nilai P(A) secara matematis ditulis sebagai berikut:

Apabila P(A) = 0, maka kejadian A merupakan kejadian mustahil, maka peluangnya merupakan 0
Contoh:
Matahari terbit di sebelah selatan merupakan kejadian mustahil, maka peluangnya = 0
Apabila P(A) = 1, maka kejadian A merupakan kejadian pasti
Contoh:
Makhluk yang bernyawa pasti mati merupakan kejadian pasti, maka peluangnya = 1
Ada juga peluang kejadian yang bernilai antara 0 dan 1, berarti kejadian tersebut mungkin terjadi. Contohnya peluang seorang murid menjadi juara kelas. Apabila L adalah kejadian pelengkap dari kejadian A, maka peluang kejadian L merupakan 1- peluang kejadian A. Secara matematis ditulis, ssebagai berikut;
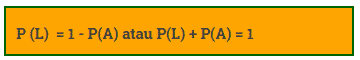
Contoh:
Apabila peluang turun hujan pada hari ini = 0,6 maka
Peluang tidak turun hujan pada hari ini = 1 – P (hujan)
= 1-0,6
= 0,4
8. Frekuensi Harapan
Frekuensi harapan suatu kejadian merupakan harapan banyaknya muncul suatu kejadian dari sejumlah percobaan yang dijalankan. Secara matematis ditulis sebagai berikut:

Contoh:
Pada percobaan melempar sebuah dadu sebanyak 60 kali, maka :
Peluang muncul mata 2 = 1/6
Frekuensi harapan muncul mata 2 = P (mata 2) x banyak percoban
= 1/6 x 60
= 10 kali
Batas-Batas Nilai Peluang
Nilai peluang suatu kejadian (P) memenuhi sifat rumus peluang kemungkinan, yang berarti Jika P = 0, maka kejadian tersebut tidak pernah terjadi atau suatu kemustahilan Jika P = 1, maka kejadian tersebut merupakan kepastian.

Jika A adalah suatu kejadian yang terjadi, dan A’ adalah suatu kejadian dimana A tidak terjadi, maka :
Contoh:
1. Sebuah dadu berbentuk mata enam dilempar sekali. Tentukan nilai peluang :
- Munculnya mata dadu bilangan asli
- Munculnya mata dadu 7
Jawab :
- Nilai peluang munculnya mata dadu bilangan asli adalah 1, karena merupakan suatu kepastian.
- Nilai peluang munculnya mata dadu 7 adalah 0, karena merupakan suatu kemustahilan
2. Dua buah dadu kubus homogen bermata enam dilempar bersama-sama sebanyak satu kali. Berapakah peluang munculnya mata dadu tidak berjumlah 12 ?
Jawab :
Banyaknya ruang sampel percobaan tersebut ada 36 kejadian, sedang kejadian muncul mata dadu berjumlah 12 ada 1 kejadian yaitu (6,6), sehingga peluang muncul mata dadu berjumlah 12 yaitu 1/36. sehingga peluang muncul mata dadu tidak berjumlah 12 yaitu 1-1/36 = 35/36
Teori Peluang
Berhubung adanya permintaan untuk menyajikan materi peluang, baru saat ini penulis mencoba membahasnya sebatas pengetahuan yang penulis peroleh, karena penulis merasa miskin akan referensi tentang peluang , selain dari itu teori peluang dalam perkembangannya lebih lanjut banyak sekali teorema-teorema yang tidak mudah untuk dicerna penulis sendiri dan mudah hilang dari ingatan yang akhirnya penulis sering menggunakan ingatan seadanya saat menjawab soal peluang. Setelah penulis memperoleh buku referensi dari kakanda dan membacanya , saya mencoba berbagi mengenai teori peluang sebatas yang saya pahami. Saya percaya siswa yang masih muda, berbekal pemahaman teori peluang yang cukup, latihan yang cukup dan kontinu akan meningkatkan kemampuan mengingat materi ini (retensi) secara lebih lama. Karena unsur atau elemen yang dibahas dalam teori peluang ini adalah himpunan berhingga maka sebagai materi prasyarat atau materi yang harus dipahami terlebih dulu yaitu operasi irisan dan gabungan dua himpunan. Simak uraian berikut !
Nilai Peluang
Contoh Soal Peluang
Berikut ini adalah beberapa contoh peluang yaitu:
1. Soal Pertama
Apabila kita melempar sebuah dadu sebanyak satu kali, tentukan peluang munculnya mata dadu 4 ?
Penyelesaian:
Banyaknya anggota/ruang sampel : n(s) = 6
Titik sampel mata dadu bernilai 4 : n(A) = 1
Rumus untuk mencari peluang munculnya mata dadu 4
P(A) = n(A)/n(S)
⇔ P(4) = 1/6
Jadi, peluang munculnya mata dadu 4 adalah 1/6
2. Soal Kedua
Hitunglah peluang terambilnya kartu As dari sebuah permainan kartu bridge ?
Penyelesaian:
Banyaknya anggota/ruang sampel : n(S) = 52
Titik sampel kartu as: n(A) = 4
Peluang terambilnya kartu As :
P(A) = 4/52 = 1/13
Jadi, peluang terambilnya kartu As adalah : 1/13
Demikian Penjelasan Materi Tentang Peluang Adalah: Pengertian, Sejarah, Rumus, Batas, Teori, Nilai dan Contoh Semoga Materinya Bermanfaat Bagi Siswa-Siswi.
The post Peluang Adalah first appeared on PAKDOSEN.CO.ID.
Bagaimana apakah Ulasan Tentang Peluang Adalah sudah cukup untuk mengobati rasa penasaran Anda? Semoga saja demikian adanya. Terima kasih sudah meluangkan waktu mampir ke situs garenggati . blogspot . com serta membaca ulasan diatas hingga selesai. Kedepannya kami akan terus mengupdate artikel pendidikan, materi pelajaran dan informasi menarik lainnya. Untuk itu pantengin terus situs ini, kalau perlu bookmark supaya Anda mudah menemukannya lagi bila suatu saat membutuhkannya. ARTIKEL PILIHAN PEMBACA :
Posting Komentar untuk "Pembahasan: Peluang Adalah ~ Garenggati"