Pembahasan: Sudut Pusat dan Sudut Keliling ~ Garenggati
Dimana ada kemauan disitu ada jalan. Pepatah ini memang terlihat sepele, tapi bermakna sangat dalam. Buktinya Anda berhasil menemukan informasi mengenai Sudut Pusat dan Sudut Keliling yang sengaja kami hadirkan untuk sobat pembaca semuanya. Disini kita akan mengulasnyya secara lengkap dan menuliskannya dengan bahasa yang mudah dimengerti sehingga akan lebih mudah dalam memahaminya. Oke langsung disimak aja yuk.
Uraian Lengkap Sudut Pusat dan Sudut Keliling
Selamat datang di Dosen.co.id, web digital berbagi ilmu pengetahuan. Kali ini PakDosen akan membahas tentang Sudut Pusat dan Sudut Keliling? Mungkin anda pernah mendengar kata Sudut Pusat dan Sudut Keliling? Disini PakDosen membahas secara rinci tentang pengertian, hubungan, rumus, unsur, sifat, cara dan contoh. Simak Penjelasan berikut secara seksama, jangan sampai ketinggalan.
Pengertian Sudut Pusat dan Sudut Keliling
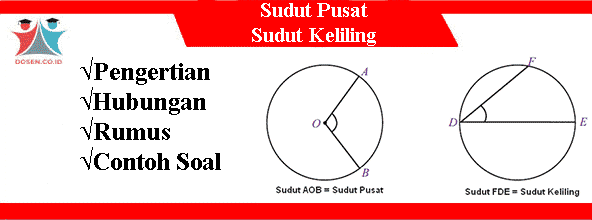
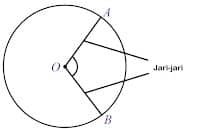
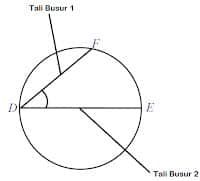
Sudut Pusat merupakan sudut yang dibentuk oleh dua jari-jari dan berbentuk pada inti lingkaran. (Lihat gambar: 1). Sudut Keliling merupakan sudut yang dibentuk oleh dua tali busur yang berbentuk di satu titik pada keliling lingkaran. (Lihat gambar: 2)
Hubungan Antara Sudut Pusat dan Sudut Keliling
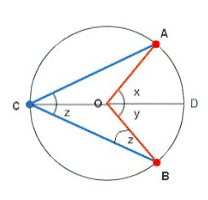
Perhatikan pada gambar diatas, bawah sudut AOB adalah sudut pusat dan sudut ACB merupakan sudut keliling yang menghadap busur yang sama yaitu busur AB. Kita akan mempelajari hubungan antara sudut pusat dan sudut keliling yang menghadap busur yang sama.
Lingkaran di samping memiliki jari-jari OA, OB, OC, OD = r
Misal : sudut AOD = x dan sudut DOB = y, maka besar sudut AOB = sudut AOD + sudut DOB = x + y
Perhatikan Segitiga BOC!
Sudut BOC pelurus bagi sudut DOB maka sudut BOC + sudut DOB = 180°, sehingga sudut BOC = 180° – sudut DOB = 180° – y.
Segitiga BOC adalah segitiga kaki, karena OC dan OB adalah jari-jari lingkaran, sehingga besar sudut OBC dan OCB sama (misal z).
Sudut OBC + sudut OCB + sudut BOC = 180°
z + z + (180° – y) = 180°
2z – y + 180° = 180°
2z = 180° – 180° + y
2z = y
z = ½ y
Sekarang perhatikan segitiga AOC!
Sudut AOC pelurus bagi sudut AOD maka sudut AOC + sudut AOD = 180°, sehingga sudut AOC = 180° – sudut AOD = 180° – x.
Segitiga AOC merupakan segitiga kaki, karena OA dan OC adalah jari-jari lingkaran, sehingga besar sudut OAC dan OCA sama (misal p).
Sudut OAC + sudut OCA + sudut AOC = 180°
p + p + (180° – x) = 180°
2p – x + 180° = 180°
2p = 180° – 180° + x
2p = x
p = ½ x
Dengan demikian, sudut ACB = sudut OCB + sudut OCA = z + p = ½ y + ½ x = ½ (x + y) = ½ sudut AOB. Maka besar sudut AOB = 2 x sudut ACB.
Karena sudut ACB adalah sudut keliling lingkaran dan sudut AOB sudut pusat lingkaran, maka dapat ditarik kesimpulan, yakni :
“Jika sudut pusat dan sudut keliling lingkaran menghadap busur yang sama, Maka besar sudut pusat = 2 kali besar sudut keliling”
Unsur-unsur Lingkaran
1. Pusat lingkaran
Merupakan titik tengah pada lingkaran yang biasa di sebut dengan pusat pada lingkaran. Jarak dari pusat lingkaran dengan titik terluar lingkaran akan sama dengan titik-titik terluar lainnya.
2. Diameter lingkaran
Merupakan garis lurus dari titik terluar lingkaran yang melewati pusat hingga titik terluar lingkaran. Diameter merupakan dua (2) kali dari jari-jari lingkaran (2 x jari-jari).
3. Jari-jari lingkaran
Merupakan jarak dari pusat lingkaran ke titik terluar lingkaran. Jari-jari lingkaran merupakan setengah dari diameter lingkaran (1/2 x diameter).
4. Busur lingkaran
5. Tali busur lingkaran
6. Temberang
7. Juring
8. Apotema
9. Sudut pusat
Sifat-sifat Lingkaran
- Mempunyai satu (1) buah sisi atau dengan kata lain terdiri dari satu (1) sisi saja.
- Mempunyai simetri putar yang tak terhingga.
- Mempunyai simetri lipat serta sumbu yang tak terhingga.
- Tidak memiliki titik sudut.
Cara Menghitung Perubahan Luas dan Keliling Jika Jari-jari Berubah
Misalkan sebuah lingkaran memiliki jari-jari r1 akan diperbesar sehingga jari-jarinya menjadi r2 dimana r2 > r1. Jika luas lingkaran semula adalah L1 serta luas lingkaran setelah mengalami perubahan jari-jari adalah L2 maka selisih luas kedua lingkaran tersebut adalah sebagai berikut.
L2 – L1 = πr2² – πr1²
L2 – L1 = π (r2² – r1²)
L2 – L1 = π (r2 – r1) (r2+r1)
Apabila keliling lingkaran semula adalah K1 selanjutnya keliling setelah mengalami perubahan jari-jari adalah K2 maka selisih keliling kedua lingkaran adalah sebagai berikut.
K2 – K1 = 2πr2 – 2πr1
K2 – K1 = 2π (r2 – r1)
Kita juga dapat menghitung perbandingan luas serta keliling limgkaran jika besarnya jari-jari berubah.
Perbandingan luas kedua lingkaran tersebut yaitu sebagai berikut.
L2 : L1 = πr2² : πr1²
L2 : L1 = r2² : r1²
selanjutnya perbandingan kelilingnya yaitu sebagai berikut.
K2 : K1 = 2πr2 : 2πr1
K2 : K1 = r2 : r1
Berdasarkan uraian tersebut kita dapat simpulkan bahwa lingkaran yang berjari-jari r1, setelah mengalami perubahan jari-jari menjadi r2 dimana r2>r1 maka selisih dan perbandingan luas serta kelilingnya sebagai berikut.
L2 – L1 = π (r2 – r1) (r2 + r1)
K2 – K1 = 2π (r2 – r1)
L2 : L1 = r2² : r1²
K2 : K1 = r2 : r1
Contoh Soal

Pada gambar di atas diketahui besar sudut ACB = 27°
hitung besar sudut AOB…!!!
Jawab:
Besar sudut AOB (sudut pusat) = 2 x ACB (sudut keliling)
= 2 x 27°
=54°
Demikian Penjelasan Materi Tentang Sudut Pusat dan Sudut Keliling: Pengertian, Hubungan, Rumus, Unsur, Sifat, Cara dan Contoh Semoga Materinya Bermanfaat Bagi Siswa-Siswi.
The post Sudut Pusat dan Sudut Keliling first appeared on PAKDOSEN.CO.ID.
Bagaimana apakah Ulasan Tentang Sudut Pusat dan Sudut Keliling sudah cukup untuk mengobati rasa penasaran Anda? Semoga saja demikian adanya. Terima kasih sudah meluangkan waktu mampir ke situs garenggati . blogspot . com serta membaca ulasan diatas hingga selesai. Kedepannya kami akan terus mengupdate artikel pendidikan, materi pelajaran dan informasi menarik lainnya. Untuk itu pantengin terus situs ini, kalau perlu bookmark supaya Anda mudah menemukannya lagi bila suatu saat membutuhkannya. ARTIKEL PILIHAN PEMBACA :





Posting Komentar untuk "Pembahasan: Sudut Pusat dan Sudut Keliling ~ Garenggati"